Trigonometric formulas and identities for class 10
The six trigonometric ratios
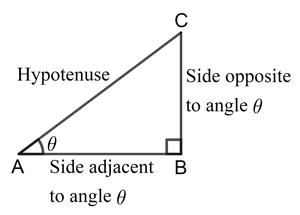
| \[1. \space sin \spaceθ = {Side \space opposite \space to \spaceθ\over Hypotenuse}\] | 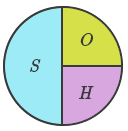 |
\[2. \space cos \spaceθ = {Side \space adjacent \space to \spaceθ\over Hypotenuse}\] | 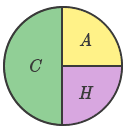
|
| \[3. \space tan \spaceθ = {Side \space opposite \space to \spaceθ\over \space Side \space adjacent \space to \spaceθ}\] | 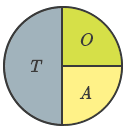
|
\[4. \space cosecant \spaceθ = {1\over sin\spaceθ}\] | 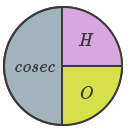
|
| \[5. \space secant \spaceθ = {1\over cos \spaceθ}\] | 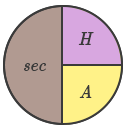
|
\[6. \space cot \spaceθ = {1\over tan \spaceθ}\] | 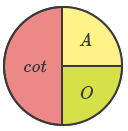
|
Trigonometric ratios of some specific angles
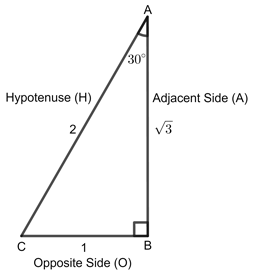
Fig.1
|
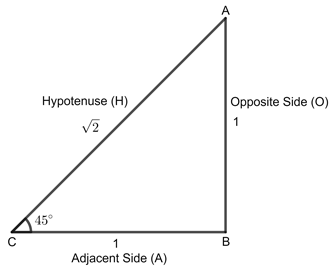
Fig.2
|
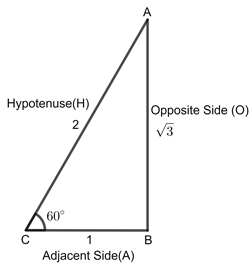
Fig.3
|
| Specific angles & Trigonometric ratios |
\[{θ \space = \space 0°}\] | \[{θ \space = \space 30°}\] | \[{θ \space = \space 45°}\] | \[{θ \space = \space 60°}\] | \[{θ \space = \space 90°}\] |
|---|---|---|---|---|---|
| \[{sin \space θ}\] | \[{0}\] | \[{1\over 2}\] | \[{1\over \sqrt{2}}\] | \[{\sqrt{3} \over 2}\] | \[{1}\] |
| \[{cos \space θ}\] | \[{1}\] | \[{\sqrt{3} \over 2}\] | \[{1\over \sqrt{2}}\] | \[{1\over 2}\] | \[{0}\] |
| \[{tan \space θ}\] | \[{0}\] | \[{1\over \sqrt{3}}\] | \[{1}\] | \[{\sqrt{3}}\] | \[{Not\space defined}\] |
| \[{cosec \space θ}\] | \[{Not\space defined}\] | \[{2}\] | \[{\sqrt{2}}\] | \[{2\over \sqrt{3}}\] | \[{1}\] |
| \[{sec \space θ}\] | \[{1}\] | \[{2\over \sqrt{3}}\] | \[{\sqrt{2}}\] | \[{2}\] | \[{Not\space defined}\] |
| \[{cot \space θ}\] | \[{Not\space defined}\] | \[{\sqrt{3}}\] | \[{1}\] | \[{1\over \sqrt{3}}\] | \[{0}\] |
Trigonometric ratios of complementary angles
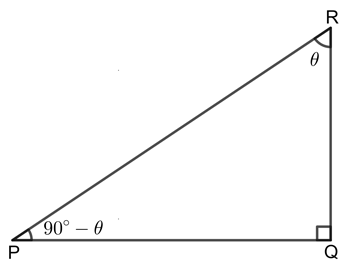
Angle \(θ\) and \((90° - θ\))are complementary angles
| \[{sin \space θ = \space cos \space (90°-θ)}\] | \[{cos \space θ = \space sin \space (90°-θ)}\] | \[{tan \space θ = \space cot \space (90°-θ)}\] |
| \[{cosec \space θ = \space sec \space (90°-θ)}\] | \[{sec \space θ = \space cosec \space (90°-θ)}\] | \[{cot \space θ = \space tan \space (90°-θ)}\] |
Trigonometric identities
| \[{sin^2 \space θ + \space cos^2 \space θ \space= \space 1}\] | \[{1+tan^2 \space θ = \space sec^2\space θ}\] | \[{1+cot^2 \space θ = \space cosec^2\space θ}\] |
Alternate forms 1:
| \[{cos^2 \space θ = \space 1 - \space sin^2 \space θ}\] | \[{sec^2 \space θ - \space tan^2 \space θ \space = \space 1}\] | \[{cosec^2 \space θ - \space cot^2 \space θ \space = \space 1}\] |
| \[{sin^2 \space θ = \space 1 - \space cos^2 \space θ}\] | \[{sec^2 \space θ - \space 1 \space = \space tan^2 \space θ}\] | \[{cosec^2 \space θ - \space 1 \space = \space cot^2 \space θ}\] |
Alternate forms 2:
| \(sin \space θ\) in terms of \(cos \space θ, \space tan \spaceθ\) | \[sin θ = {\sqrt{1-cos^2θ}}\] | \[sin θ = {tanθ \over \sqrt{1-tan^2θ}}\] |
| \(cos \space θ\) in terms of \(sin \space θ, \space tan \spaceθ\) | \[cos θ = {\sqrt{1-sin^2θ}}\] | \[cos θ = {1\over \sqrt{1+tan^2θ}}\] |
| \(tan \space θ\) in terms of \(sin \space θ, \space cos \space θ\) | \[tan θ = {sin θ \over \sqrt{1-sin^2θ}}\] | \[cos θ = {\sqrt{1+cos^2θ} \over cosθ }\] |
